Important: The GCConnex decommission will not affect GCCollab or GCWiki. Thank you and happy collaborating!
Difference between revisions of "RATTWiki"
| Line 46: | Line 46: | ||
A more detailed description of the probability distributions and the required parameters to define them follows. | A more detailed description of the probability distributions and the required parameters to define them follows. | ||
| − | '''Distribution Types''' | + | ==== '''Distribution Types''' ==== |
| − | |||
| − | |||
| + | ===== '''Normal''' ===== | ||
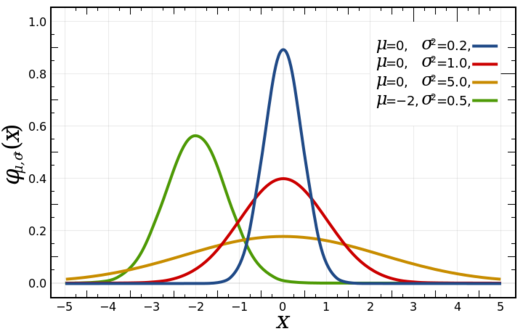
One of the most familiar continuous probability distributions is the normal distribution as shown in Figure 2. The normal distribution is also known as the Gaussian distribution or the bell curve. It is a very common distribution in nature and statistics and is based on the central tendency theory. This is a situation where most items in a group tend towards the average and the further away from the average an event is the less likely it is to occur. | One of the most familiar continuous probability distributions is the normal distribution as shown in Figure 2. The normal distribution is also known as the Gaussian distribution or the bell curve. It is a very common distribution in nature and statistics and is based on the central tendency theory. This is a situation where most items in a group tend towards the average and the further away from the average an event is the less likely it is to occur. | ||
[[File:Figure 3.svg|center|thumb|523x523px|Figure 3: Normal Distributions]] | [[File:Figure 3.svg|center|thumb|523x523px|Figure 3: Normal Distributions]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
To define a normal distribution only two parameters are needed: the mean and the variance (standard deviation). | To define a normal distribution only two parameters are needed: the mean and the variance (standard deviation). | ||
| − | + | ===== '''Flat (Uniform)''' ===== | |
| − | |||
In a flat distribution any value between a defined minimum and maximum are possible and equally likely. The outcome within the defined range is completely random. | In a flat distribution any value between a defined minimum and maximum are possible and equally likely. The outcome within the defined range is completely random. | ||
| − | Figure 4: Flat (continuous uniform) Distribution | + | [[File:Fig 4.png|center|thumb|517x517px|Figure 4: Flat (continuous uniform) Distribution]] |
As can be seen Figure 4, to define this distribution only 2 parameters are required. They are '''a''' (the minimum possible outcome) and '''b''' (the maximum possible outcome). | As can be seen Figure 4, to define this distribution only 2 parameters are required. They are '''a''' (the minimum possible outcome) and '''b''' (the maximum possible outcome). | ||
| − | + | ===== '''Triangular''' ===== | |
The triangular distribution is typically used as a subjective description of a population for which there is only limited sample data, and especially in cases where the relationship between variables is known but data is scarce (possibly because of the high cost of collection). It is based on knowledge of the minimum and maximum and an "inspired guess" as to the modal value. | The triangular distribution is typically used as a subjective description of a population for which there is only limited sample data, and especially in cases where the relationship between variables is known but data is scarce (possibly because of the high cost of collection). It is based on knowledge of the minimum and maximum and an "inspired guess" as to the modal value. | ||
| + | [[File:Fig 5.png|center|thumb|577x577px|Figure 5; Triangular Distribution]] | ||
| + | Because of its application as a default distribution to use when little data is available, the triangle distribution is very useful when a model parameter is selected based on solicitation of expert opinion. The triangular distribution looks something like that is shown in Figure 5. The parameters required for this distribution are the lowest possible value (the minimum – '''a'''), the most likely value (the mode – '''c'''), and the highest possible value (the maximum – '''b'''). | ||
| − | + | ===== '''Defined''' ===== | |
| − | |||
| − | |||
| − | |||
| − | + | The defined distribution is essentially a discrete distribution where any number of sets of outcomes and their probabilities can be created – as long as the probabilities of all outcomes sum to 1. This can be useful in situations where there is a variable or outcome associated with a worse case scenario (pessimistic), a most likely scenario (realistic), and a best-case scenario (optimistic) as can be seen in Figure 6. | |
| − | + | [[File:Fig 6.png|center|frame|Figure 6 Discrete Defined Distribution]] | |
| − | + | To define this distribution three sets of the outcome and probabilities are required. These are entered into RRAT by first entering the value followed by a comma and then the probability. Individual outcome and probability sets are separated by semi-colons. | |
| − | + | * '''Outcome1,Probability1;Outcome2,Probability2;….OutcomeN,ProbabilityN''' | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | '''Outcome1,Probability1;Outcome2,Probability2;….OutcomeN,ProbabilityN''' | ||
| Line 102: | Line 89: | ||
Sets of outcomes are then divided by a semi-colon. For instance, we may want to make three economic growth forecasts, one based on 1% GDP growth (pessimistic), with a 10% likelihood, one based on 3% GDP growth (realistic) with a likelihood of 70% and one based on 5% GDP growth (optimistic) with a 20% likelihood. | Sets of outcomes are then divided by a semi-colon. For instance, we may want to make three economic growth forecasts, one based on 1% GDP growth (pessimistic), with a 10% likelihood, one based on 3% GDP growth (realistic) with a likelihood of 70% and one based on 5% GDP growth (optimistic) with a 20% likelihood. | ||
| − | |||
These parameters would be entered in RRAT as ''0.01,0.1;0.03,0.7;0.05,0.2''. Note that the sum of the probabilities of the outcome sets must equal 1 to fully define the distribution. This function can be used to describe any probabilistic discrete distribution outcome. For instance a coin toss (''heads,0.5;tails,0.5''), a dice role (''1,0.1666666'';2, ''0.1666666;3,0.1666666'';4, ''0.1666666;5,0.1666666;6,0.1666666)'' and many others. | These parameters would be entered in RRAT as ''0.01,0.1;0.03,0.7;0.05,0.2''. Note that the sum of the probabilities of the outcome sets must equal 1 to fully define the distribution. This function can be used to describe any probabilistic discrete distribution outcome. For instance a coin toss (''heads,0.5;tails,0.5''), a dice role (''1,0.1666666'';2, ''0.1666666;3,0.1666666'';4, ''0.1666666;5,0.1666666;6,0.1666666)'' and many others. | ||
| − | + | ===== '''Fixed''' ===== | |
| − | |||
| Line 114: | Line 99: | ||
Once you have given the variable a description, selected the distribution type, and defined the parameters of the distribution for every item you have completed the first stage. Every time a simulation is run by RRAT a value will be drawn from the probability distributions defined and entered in '''column C''' next to the description. As these are the values that will be used in other formulas in the spreadsheet it is highly recommended that you name these cells appropriately to make them easier to reference. To determine how to name a cell in Excel, refer to your Excel help function. | Once you have given the variable a description, selected the distribution type, and defined the parameters of the distribution for every item you have completed the first stage. Every time a simulation is run by RRAT a value will be drawn from the probability distributions defined and entered in '''column C''' next to the description. As these are the values that will be used in other formulas in the spreadsheet it is highly recommended that you name these cells appropriately to make them easier to reference. To determine how to name a cell in Excel, refer to your Excel help function. | ||
| − | + | [[File:Fig 7.png|none|thumb|1160x1160px|Figure 7: Naming a Cell]] | |
| − | Figure 7: Naming a Cell | ||
| − | |||
In the above example (Figure 7) a defined distribution has been used with a low population growth rate of 1% having a 40% probability, medium population growth rate of 3% at 50% probability, and a high population growth rate of 5% at 10% probability. Each time a simulation is run either 1%, 3%, or 5% will be entered into cell C9. To make it easier to reference this value in related formulas the cell is named “'''POPGrow”.''' After the cell has been named it is now possible to refer to it by its name rather than by a cell reference such as “C9”. This will make the next stage in the process much easier and makes your spreadsheets easier to understand, both for yourself and reviewers. | In the above example (Figure 7) a defined distribution has been used with a low population growth rate of 1% having a 40% probability, medium population growth rate of 3% at 50% probability, and a high population growth rate of 5% at 10% probability. Each time a simulation is run either 1%, 3%, or 5% will be entered into cell C9. To make it easier to reference this value in related formulas the cell is named “'''POPGrow”.''' After the cell has been named it is now possible to refer to it by its name rather than by a cell reference such as “C9”. This will make the next stage in the process much easier and makes your spreadsheets easier to understand, both for yourself and reviewers. | ||
Revision as of 11:03, 21 July 2025
Regulatory Risk Analysis Tool - Monte Carlo Simulation
Introduction & Motivation
When conducting a Cost Benefit Analysis (CBA) the assessment model is often based on assumptions or parameters that are uncertain. Knowledge of how uncertainties impact outcomes provide important information that deepens our understanding beyond just the most likely outcome. In the case of only one uncertain parameter, it is a relatively simply process to determine how alternative possibilities affect the outcome, however as the number of uncertain/risky parameters increases the range of possible outcomes that may result from a particular combination increases to a magnified level.
When outcomes are not discrete (one possible outcome among a limited set of possibilities) but continuous (one possible outcome among unlimited possibilities with or without a range) the problem becomes even more complex. As most parameters are of a continuous nature a more robust method than traditional sensitivity analysis is needed.
In situations such as this model inputs may be best defined as probability distributions rather than an individual number. When more than one probability distribution is used in repeated simulations to calculate an objective outcome this is referred to as a Monte-Carlo experiment. This works by repeatedly and randomly selecting outcomes from the distributions of the various inputs and applying them to the model. Each time this is done, a possible outcome of the model is created. The more times this process is repeated the more observations from the total set of possible outcomes are calculated, until eventually enough data is collected to piece together a probability-distribution of the model output.
This process can be seen in the above figure where three model parameters exist, and each parameter is represented by a probability distribution. By applying the Monte-Carlo method, model outputs can also be represented by a probability distribution. In the case of a CBA this process would allow us to make statements such as what is the probability that the Net Present Value (NPV) of a regulatory proposal will be above zero (there is a 95% probability that the regulations benefits would exceed its costs), a confidence interval of the NPV (90% of the time the regulations would provide a NPV of between $50 and $90 million), the standard deviation of the NPV, the average NPV, the most likely outcome NPV, and which parameters are likely to have the greatest impact on the NPV.
Because uncertainty and risk in an outcome can be considered as a cost itself, this information adds important insight towards improving program choice and implementation of a regulation. In many cases costs need to be incurred to decrease uncertainties and thus the regulatory option with the central or expected highest net-present value may not always be the preferred option if it is important to limit our exposure to risk. This can be particularly important for outcomes that are discontinuous due to thresholds or irreversible outcomes that can result in low probability but high impact outcomes.
While Monte-Carlo methods have been around for a long time it is only with the increase of computing power that this kind of analysis has become common. Today there are many statistical programs that can perform Monte-Carlo simulations. While these packages are powerful and feature rich, they may not be accessible to all analysts within the Federal Government. They can be expensive and require special knowledge and training. Furthermore, the human resources required to acquire such packages through government acquisition services can become a barrier to the average analyst. It also becomes difficult to share models created with these software packages with other analysts or departments to confirm reported results or adjust parameters for further analysis as they will need to have the necessary software to do so.
It is for these reasons that I endeavoured to create a simple solution to enable Monte Carlo simulation analysis. The Regulatory Risk Analysis Tool (RRAT) works within Microsoft Excel using visual basic macros. This permits analysts to work within an environment that they are familiar with and does not require the acquisition of any additional software licenses. It also allows the tool to be incorporated into existing models in excel, increasing their functionality. While it is not as powerful a tool as other commercial software packages, it should fill the needs of most regulatory CBAs, and since it is open-source code, its capacities can be expanded and improved as required by others that may wish to do so.
Steps to Setting up a Simulation
Preliminary Steps: Prepare Excel for RRAT
Before using RRAT there are a few things that need to be checked. First, the RRAT is a Microsoft Excel application, as it works by using macros, you will have to ensure that your security settings on Excel allows for these to run. The procedures for this differ depending on the version of Excel you are using and the security protocols your department have in place.
RRAT also makes use of certain functions from Excel Add-Ins. Thus, before running the simulation you should check that the Solver Add-In, the Analysis ToolPak & Analysis ToolPak VBA are active in your Excel program (File - Options - Add-Ins).
RRAT includes two sheets that are referred to by macros. These sheets are called “Model Inputs” and “Model Outputs” any number of additional sheets can be added or copied into the RRAT but “Model Inputs” must always be the 1st sheet in the tab list and “Model Outputs” must be the second
Stage 1: Define Distributions for Independent Outcomes with Uncertainty
The first step in setting up the simulation will be to define what variables you are interested in examining the impact of uncertainty on the outcome of the CBA. Enter the description for each of these variables starting in cell B9 on the Model Inputs sheet. It is important that a description be entered here as a blank entry in the description column is used as a signal to the program that no more entries exist. The area on the sheet to enter descriptions can be seen in Figure 2 in the area labelled as “A”.
The second step in the setting up the simulation will be to define the probability distributions for the independent variable inputs. While there are numerous probability distributions used in Monte-Carlo, RRAT is currently limited to five, although this limitation can be overcome by combining distributions.
Two of these are discrete distributions and three are continuous. The continuous distributions used are the normal, triangle and the flat (continuous uniform). The discrete distributions are defined (discrete) and fixed (one non-varying constant). The probability distributions need to be selected from a pull-down option from the column under the heading “Distribution Type” (column D) on the Model Inputs sheet (Figure 2 – Area “B”).
The final stage in defining a distribution is entering in their parameters. These parameters differ depending on the type of distribution selected and are displayed in the table above the columns where they are entered (columns E – F – G). When a distribution type is selected areas that do not need to be defined are blacked out. For instance, in Figure 2 the normal distribution has been selected. As a result, in area “C” where the distribution parameters are entered the first parameter has been blackened out. From the table above you can see that the mean of the distribution needs to be entered in column F and the variation needs to be entered in column G.
A more detailed description of the probability distributions and the required parameters to define them follows.
Distribution Types
Normal
One of the most familiar continuous probability distributions is the normal distribution as shown in Figure 2. The normal distribution is also known as the Gaussian distribution or the bell curve. It is a very common distribution in nature and statistics and is based on the central tendency theory. This is a situation where most items in a group tend towards the average and the further away from the average an event is the less likely it is to occur.
To define a normal distribution only two parameters are needed: the mean and the variance (standard deviation).
Flat (Uniform)
In a flat distribution any value between a defined minimum and maximum are possible and equally likely. The outcome within the defined range is completely random.
As can be seen Figure 4, to define this distribution only 2 parameters are required. They are a (the minimum possible outcome) and b (the maximum possible outcome).
Triangular
The triangular distribution is typically used as a subjective description of a population for which there is only limited sample data, and especially in cases where the relationship between variables is known but data is scarce (possibly because of the high cost of collection). It is based on knowledge of the minimum and maximum and an "inspired guess" as to the modal value.
Because of its application as a default distribution to use when little data is available, the triangle distribution is very useful when a model parameter is selected based on solicitation of expert opinion. The triangular distribution looks something like that is shown in Figure 5. The parameters required for this distribution are the lowest possible value (the minimum – a), the most likely value (the mode – c), and the highest possible value (the maximum – b).
Defined
The defined distribution is essentially a discrete distribution where any number of sets of outcomes and their probabilities can be created – as long as the probabilities of all outcomes sum to 1. This can be useful in situations where there is a variable or outcome associated with a worse case scenario (pessimistic), a most likely scenario (realistic), and a best-case scenario (optimistic) as can be seen in Figure 6.
To define this distribution three sets of the outcome and probabilities are required. These are entered into RRAT by first entering the value followed by a comma and then the probability. Individual outcome and probability sets are separated by semi-colons.
- Outcome1,Probability1;Outcome2,Probability2;….OutcomeN,ProbabilityN
Where: Probability1 + Probability2 + … + ProbabilityN = 1.00
Sets of outcomes are then divided by a semi-colon. For instance, we may want to make three economic growth forecasts, one based on 1% GDP growth (pessimistic), with a 10% likelihood, one based on 3% GDP growth (realistic) with a likelihood of 70% and one based on 5% GDP growth (optimistic) with a 20% likelihood.
These parameters would be entered in RRAT as 0.01,0.1;0.03,0.7;0.05,0.2. Note that the sum of the probabilities of the outcome sets must equal 1 to fully define the distribution. This function can be used to describe any probabilistic discrete distribution outcome. For instance a coin toss (heads,0.5;tails,0.5), a dice role (1,0.1666666;2, 0.1666666;3,0.1666666;4, 0.1666666;5,0.1666666;6,0.1666666) and many others.
Fixed
The fixed distribution is essentially one outcome that has 100% chance of occurring. It is the same as a constant and does not need to be defined here except that it is useful for the analyst to collect key assumptions of the model into one area. This also facilitates changing what was first assumed to be constant in a model to later evaluate uncertainty in that constant if deemed necessary.
Once you have given the variable a description, selected the distribution type, and defined the parameters of the distribution for every item you have completed the first stage. Every time a simulation is run by RRAT a value will be drawn from the probability distributions defined and entered in column C next to the description. As these are the values that will be used in other formulas in the spreadsheet it is highly recommended that you name these cells appropriately to make them easier to reference. To determine how to name a cell in Excel, refer to your Excel help function.
In the above example (Figure 7) a defined distribution has been used with a low population growth rate of 1% having a 40% probability, medium population growth rate of 3% at 50% probability, and a high population growth rate of 5% at 10% probability. Each time a simulation is run either 1%, 3%, or 5% will be entered into cell C9. To make it easier to reference this value in related formulas the cell is named “POPGrow”. After the cell has been named it is now possible to refer to it by its name rather than by a cell reference such as “C9”. This will make the next stage in the process much easier and makes your spreadsheets easier to understand, both for yourself and reviewers.
Note 2: RRAT already contains several named cells that are “reserved”. No data check is performed to preserve this reserved status but changing them is likely to result in RRAT failure these names are:
- CDIS
- Distributions
- NumSims
- numvar
- para1
- para2
- para3
- para1val
- para2val
- para3val
In addition, cell references can not contain a space.
1.1.1 Entering a Distribution by Form
As an alternative to manually entering a distribution directly into the spreadsheet you can add a distribution by form. The form can be opened by pressing the “Manage Assumptions” button as in Figure 7 (below the picture of a mouse). This will open the form shown in Figure 8.
Figure 8: Adding a distribution by form
The information to define a distribution can be entered in this form and added to the spreadsheet. In addition, if an entry is added to the “Reference Name” field this name will be assigned to the value cell automatically. Also, the titles for the parameters of the distributions will change dynamically depending on what distribution type is selected to make it more clear what data is required.
You can also use this form to edit previously entered distribution. Do this by clicking on the distribution in the list. The fields in the form will now be dynamically linked to the values in the spreadsheet.
To assist the user in making a defined distribution, which can have many parameters, RRAT has an additional custom form that can be used to help (See Figure 9: Creating a Defined Distribution). This form can be used by entering an outcome/probability combination and then clicking ‘Add Outcome’ repeatedly until all discrete outcomes are added. Once the probability of all outcomes totals 1, the ‘Add Distribution’ button can be clicked and the distribution will be added to the form in the required format (outcome,probability;…).
Figure 9: Creating a Defined Distribution
1.2 Stage 2: Define Formulas for Dependent Outcomes
The next stage in setting up a Monte-Carlo simulation is to set up the equations that will be calculated based on the results pulled from the probability distributions defined in the previous stage. To demonstrate this, imagine we have defined 4 probability distributions as shown in Figure 10.
Figure 10: Demo Distributions
Here we have defined 4 distributions and one constant that will be used to calculate benefits from an imaginary regulatory proposal that reduces the risk of premature mortality. The distributions are for the population growth rate, the expected reduction in risk of premature mortality annually for the population because of the regulation, the value of a statistical life, the discount rate, and some related program cost. In this case the discount rate will not actually vary, but you can see how it is useful to list all the major assumptions in one place. If you refer to the one value here in all of the equations that reference it, then it becomes much easier to change that assumption at a later date.
The cells D9:D13, where the values pulled from the probability distributions defined for each simulation will be placed have been named POPGrow, RedMort, VSL, Discount, and ProgCost respectively. When using the custom form to create distributions, RRAT puts references to these names in row H. This makes it easier to use these parameter names in the rest of the spreadsheet where calculations will be made to estimate the benefits of the regulation. This can be seen in Figure 11 in the model where formulas have been calculated using these named cells.
Figure 11: Demo Model
In cell B3 an initial population for Canada of 34 million has been entered. The rest of the cells are calculated as follows:
- the population in 2011 (Cell B4): “=B3*(1+POPGrow)”
- the reduced number of premature fatalities(C4): “=B4*RedMort”
- the monetized value of the risk reduction (D4): “=C4*VSL”
- the discounted value for that benefit (Cell E4): “=D4/(1+Discount)^(A4-$A$3)
The equations from row 4 are then copied and pasted into the rest of the rows in the table. At the very bottom right-hand side of the table the present value of the benefit is calculated as the sum of all the cells above it.
Although this is a relatively simple model the combined uncertainty of the underlying parameters makes expressing what we would expect to result a challenge. We could just give a central estimate based on the most likely or central outcomes of each of the probability distributions defined and report a benefit of $171.86 million, but how likely is that result? Given what we know about the program cost, how confident could we be that the benefits would exceed these costs? These are the types of questions running a Monte-Carlo analysis can help us answer. But before we begin to discuss that we first need to finalize our experiment by selecting what to report in the “Model Outputs” worksheet.
1.3 Stage 3: Reporting Outcomes
Every time a simulation is run within a Monte-Carlo experiment a new set of model inputs are created and a new set of model outputs are calculated. As the number of simulations needed to get a robust sample of outputs to define a probability distribution will likely run in the thousands the total amount of data such a process generates may be overwhelming. However, not all this data will need to be recorded and it is up to the analyst to decide which sets of inputs and outputs to report.
Figure 12: Recording Outputs
This is done by using the second worksheet titled “Outputs” (Figure 10). In this worksheet all calculations from each simulation can be recorded for later analysis. This is done by:
- Entering a description for the output starting in cell C5. The first blank cell in row 5 marks the end of reporting information and no data after will be recorded.
- Entering a formula or a reference to the cell that you want to record from each simulation (Row 6).
- (Optional) Entering a customized format for the numbers to be recorded (Row 7). This formatting information is entered in the same way as you would for customized number formats within Excel (see the Excel help file for more information).
Continuing with our previous example in Figure 10, here we are reporting on the net present value. This is calculated as the sum of the discounted benefits (Cell E14 from sheet1 which was created in stage 2) minus the program costs. For this example, program costs have been defined as an additional probability distribution (normal) with a mean of $100 million and a standard deviation of $3 million. In addition to the net present-value we have requested the program to record information for each simulation of the expected statistical lives saved and the reduced risk of premature mortality.
1.4 Stage 4: Running the Simulation
The final stage is simple. First, you need to decide how many simulation runs will be sufficient. This information is entered in cell E1 of the Model Inputs sheet. This cell can be seen in Figure 10. To ensure a good sampling of the possible outcomes the simulation should be run at least a couple thousand times, although the more simulations you run, the longer it will take RRAT to complete the process.
The only thing remaining to be done is to press the “Run Simulation” button on the Inputs sheet. When this button is pressed the simulations begin and a progress bar will appear. Each time a simulation is run a new row of data is entered in the Model Outputs sheet beginning in row 19. Both the progress indicator and the data entries can be seen in Figure 13. For all but the most complicated models this process should only take a few minutes or less. If the model is large you may want to do a test run with only 100 or fewer simulations to get an idea of the time frame you may need to do a larger sampling and to make sure you have done the previous steps correctly. If the model runs slower than expected, it might be a good idea to close all other spreadsheets and remove any calculations or background data not needed for the Monte-Carlo analysis.
Figure 13: Running the Simulation
2 Analysing the Results
Depending on the data that you have decided to report in the Outputs sheet there will be several ways to analyse results from the Monte Carlo experiments that you perform. Several equations for statistics on data series generated are automatically entered when the simulation is run, and two additional functions for information on data ranges exist within RRAT. However, by using the built-in functionality of excel itself you will be able to produce a much wider array of useful information, tables, and figures that will provide insight to your CBA.
2.1 Automatically Generated Statistics
For each data series that RRAT produces in the Outputs sheet formulas will be entered to calculate the maximum outcome, the minimum outcome, the mean (average) outcome, the median outcome (the outcome in the middle), the mode (the outcome that occurs the most), and the standard deviation. These are all calculated using common excel formulas and are done automatically to save the analyst time in entering these standard statistics of interest. The area where these results are reported can be seen in Figure 12 in rows 12-17. Note that the mode, the result that occurs the most often, will often result in an error result when dealing with continuous distributions as any one particular result is unlikely to be exactly recreated. If you wish to see a mode result, you can try rounding the result for the objective output.
2.2 Ranges and Probabilities
As mentioned, one of the main purposes of Monte-Carlo analysis is to allow for the creation of a probability distribution for model outputs. This allows the analyst to make probabilistic statements about outcomes. This almost always involves not just one outcome but a range of outcomes because the probability of any one outcome when dealing with continuous distributions is close to zero. Thus, it is much more useful to discuss the probability of an outcome occurring between two points (a range) than a single event.
Once a Monte-Carlo simulation has been run we can then ask one of two questions regarding the output distributions from the simulations:
- What is the central range associated with a given probability?
- What is the probability associated with a given range?
To answer these questions two functions are available (see Figure 14).
Figure 14: Range & Probability Functions
The first function finds a central range within which a user entered percentage of the outcomes are contained. To use this function, you must first enter a percentage in Row 9 for each outcome you wish to have this calculated. The function then attempts to find an upper and a lower value between which the indicated percentage of outcomes lie. As there could be more than one solution for this question this function attempts to find the central range where there is an equal number of outcomes occurring that are greater than the upper value as there are outcomes that are less than the lower value. For example, in Figure 14, 90% has been entered and the function has determined that 90% of the outcomes occur between -$1.85 million (5% of outcomes less than -$1.85 million) and $145.19 million (5% greater). This function is triggered by the user pressing the Central Range of a Probability button. A range will then be calculated for each column where a percentage probability has been entered. It should be noted that there may be cases where a range solution for the given percentage does not exist and in such cases the function may return a result that is nonsensical and thus the result should be reviewed and confirmed.
The second function calculates the probability of an outcome occurring within a given range. In Figure 15 a range has been entered for the Net Present Value with the lower limit being 0 and the upper limit being the maximum value in the data set. Pressing the Calculate Probability of a Range button then causes the function to count each value in the data set that is greater than zero (and less than the max). The resulting 95.18% can be interpreted as the probability that the proposed regulation will result in a positive Net Present Value.
Figure 15: Probability of a Range
2.3 Creating Histograms
Within Excel’s statistical analysis tools (must be activated as an add-in) there is a function that will automatically create a histogram from data sets such as those produced while running a Monte-Carlo simulation using RRAT. The Excel tool will automatically count the number of results that occur between ranges. The ranges are called “Bins” and can by pre-defined by the user or will be automatically calculated by Excel. The tool can also be optionally told to produce a chart and calculate cumulative percentages.
The result of doing this procedure (with some additional formatting) can be seen in Figure 16. From this histogram the distribution of the results is slightly skewed towards higher NPV outcomes. This means that while the most likely outcome (the mode) is around $34 million there is a much higher probability that the result will be greater than this than less than (i.e. mode < mean). For a regulatory proposal, this information could add weight to a department’s justification for acceptance of the proposed regulation.
Figure 16: Histogram of NPV
2.4 Exporting Results/ RRAT Options
As you may wish to do additional analysis (including those discussed in the next section), RRAT has an option to export the outputs produced by the simulation to a separate spreadsheet. This option can be changed by pressing the ‘Options’ button available at the top of the ‘Model Inputs’ tab. Export data to a separate worksheet will make your main spreadsheet cleaner and preserve simulation results, since each simulation ran in RRAT clears previous results. If you select this option, RRAT can also automatically produce histograms for each distribution output (note: histograms for multiple output distributions are staked one on top of the other in the output sheet, make only the last one visible, until you move them).
The last option available is to turn on or off screen updating. Screen updating will show the spreadsheet, as it will display values as the change each time a simulation is run, which can be fun to watch, but also slows down the overall time it takes for a complete set of simulations to be completed. Setting this option off, while hide any updates as the simulation runs, speeding up the run time. Other options are likely to be added here in the future as RRAT development continues.
Figure 17: Setting Options
The last option available within RRAT is associated with the ‘CLEAR ENTRIES BUTTON’. As expected, pressing this button will clear all user entries and data created from a simulation from the spreadsheet.
2.5 Sensitivity Analysis - Exploring Relations
One of the main purposes of sensitivity analysis is to determine how variability in one assumption impacts the objective function. In terms of regulatory CBA the objective function is usually NPV. With a Monte-Carlo simulation a huge data set is produced that can be used to perform such sensitivity analysis. A good way to do this is by producing a scatter chart of the objective function versus the variable or assumption of concern.
To demonstrate this Figure 15 shows a scatter chart of the NPV vs mortality risk reduction. Note that in this case the graph is based on risk reduction rounded to one decimal place (risk reduction within a population of 10 million) rather than the exact risk reduction. As one would expect there is a clear positive relationship between the risk reduction in premature mortality caused by the regulation and NPV. It also appears that if the regulation fails to achieve a risk reduction of at least 6 in 100 million the expected NPV of the regulatory proposal is likely to be negative. On the other hand, if the risk reduction achieved is greater than 1 in 10 million, even given the uncertainty in the other assumptions, there is almost zero probability that the NPV will be negative.
Figure 18: The Effect of Risk Reduction Uncertainty on NPV
Finally, of interest is that as the risk reduction increases it also appears that the range of possible outcomes caused by uncertainty in the other assumptions (population growth rate, VSL, and the program cost), while remaining positive, increases.
Thus, from one scatter-plot we have discovered a number of very important outcomes. In a complete analysis it would require very little effort to repeat this process for other assumptions in a similar manner. Furthermore, the example used in this guide is relatively simplistic by design but the methods of analysis of outcomes using Monte-Carlo experiments will be similar no matter what the complexity of the model.
Conclusion & Next Steps
I hope that this instruction manual has given enough information for analysts familiar with cost benefit analysis and excel to be able to use the RRAT. While the tool itself is relatively simplistic as compared to other commercially available statistical analysis packages I believe this manual has demonstrated that combining its functions with the tools that are already available within Excel can provide some very powerful results and analysis that can strengthen CBA on a regulatory proposal.
Despite this there will obviously be areas for improvement in this tool as it is still very much under-development and thus the author is looking for feed-back in this area. It is also anticipated that this product will not stand alone and that it will be used in co-ordination with other CORE products designed to help Departments produce quality CBA on regulatory proposals. These other tools include the Cost Benefit Identification Session (CBIS) tool, the CBA template, and the official TBS CBA Policy and Guidelines.
For more information on this and other tools and services offered by the Centre of Regulatory Expertise please contact:
Timothy Folkins
Expert Advisor
Centre of Regulatory Expertise | Centre de compétence réglementaire
Regulatory Affairs | Affaires réglementaires
Treasury Board of Canada Secretariat | Secrétariat du Conseil du Trésor du Canada
Ottawa, Canada K1A 0R5
Timothy.Folkins@tbs-sct.gc.ca
Telephone | Téléphone 613-882-2077
Government of Canada | Gouvernement du Canada